-
Recent Posts
Tags
Aeolis Mons Arizona State University ASU atmosphere Beautiful Mars Cape Tribulation clouds craters Curiosity dunes dust Endeavour Crater ESA European Space Agency Gale Crater High Resolution Imaging Science Experiment HiRISE Malin Space Science Systems Marathon Valley MARCI Mars Color Imager Mars Exploration Rover Mars Odyssey Mars Reconnaissance Orbiter Mars Science Laboratory mass wasting MER Mount Sharp MRO MSL MSSS Murray Formation NASA Opportunity sand dunes Stimson Formation storms THEMIS THEMIS Image of the Day Thermal Emission Imaging System University of Arizona Vera Rubin Ridge volcanics weather windArchives
Links
general
mission instruments
- CRISM: Compact Reconnaissance Imaging Spectrometer for Mars
- CTX: Context Camera
- HiRISE: High Resolution Imaging Science Experiment
- MARSIS: Mars Advanced Radar for Subsurface and Ionosphere Sounding
- SHARAD: Shallow Radar
- THEMIS: Thermal Emission Imaging System
missions
- All Mars missions list
- Curiosity rover
- ExoMars
- Hope (al-Amal) orbiter
- InSight
- Mars Atmosphere and Volatile Evolution Mission (MAVEN)
- Mars Exploration Rovers (MER)
- Mars Express (MEX)
- Mars Odyssey
- Mars Orbiter Mission (MOM) / Mangalyaan
- Mars Reconnaissance Orbiter (MRO)
- Mars Science Laboratory (MSL)
- Perseverance Rover
- Tianwen-1 orbiter/rover
news
Tag Archives: lava channels
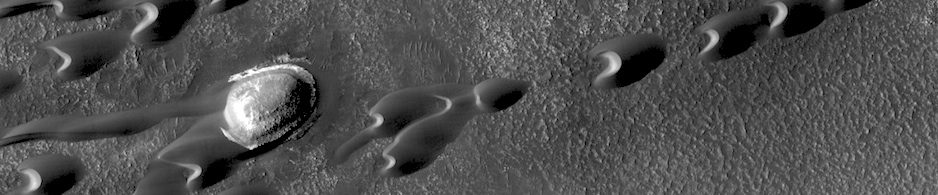
THEMIS: Lava tube takes a sharp turn
THEMIS Image of the Day, November 6, 2017. This image shows part of the eastern flank of Pavonis Mons. Surface lava flows run down hill from the upper left of the image towards the bottom right. Perpendicular to that trend … Continue reading
Posted in Reports
Tagged Arizona State University, ASU, faulting, faults, graben, lava channels, lava flows, lava tubes, Mars Odyssey, NASA, Pavonis Mons, Tharsis, THEMIS, THEMIS Image of the Day, Thermal Emission Imaging System, volcanics
Comments Off
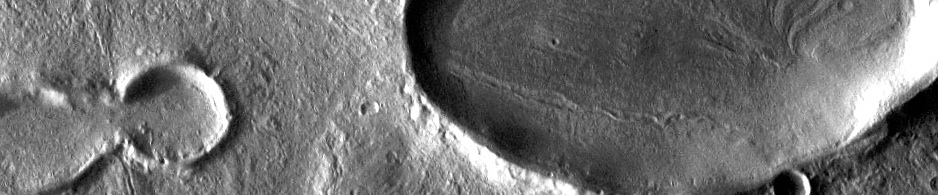
THEMIS: Collapsed lava tubes on Pavonis Mons
THEMIS Image of the Day, November 3, 2017. This image shows part of the southeastern flank of Pavonis Mons. Surface lava flows run down hill from the top left of the image to the bottom right. Perpendicular to that trend … Continue reading
Posted in Reports
Tagged Arizona State University, ASU, lava channels, lava flows, lava tubes, Mars Odyssey, NASA, Pavonis Mons, Tharsis, THEMIS, THEMIS Image of the Day, Thermal Emission Imaging System, volcanics
Comments Off
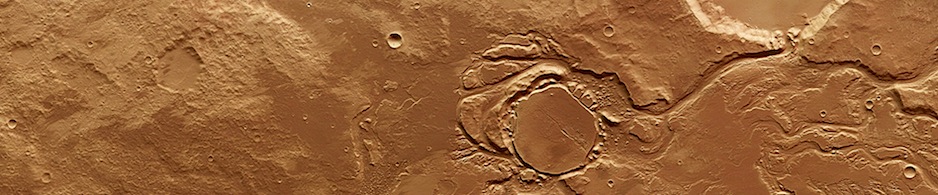
THEMIS: Collapse pits and lava tubes
THEMIS Image of the Day, November 1, 2017. This image shows part of the southern flank of Pavonis Mons. Several faults run from the left to the right side of the image. Lava flows, and the lava collapse features at … Continue reading
Posted in Reports
Tagged Arizona State University, ASU, lava channels, lava flows, lava tubes, Mars Odyssey, NASA, Pavonis Mons, Tharsis, THEMIS, THEMIS Image of the Day, Thermal Emission Imaging System, volcanics
Comments Off
THEMIS: Fractures on Pavonis Mons’ flank
THEMIS Image of the Day, October 31, 2017. This image shows part of the western flank of Pavonis Mons. The linear features are faults. Faulting usually includes change of elevation, where blocks of material slide down the fault. Paired faults … Continue reading
Posted in Reports
Tagged Arizona State University, ASU, faulting, faults, graben, lava channels, lava flows, lava tubes, Mars Odyssey, NASA, Pavonis Mons, tectonics, Tharsis, THEMIS, THEMIS Image of the Day, Thermal Emission Imaging System, volcanics
Comments Off
THEMIS: Collapsed lava tubes on Pavonis Mons
THEMIS Image of the Day, October 30, 2017. This image shows part of the southern flank of Pavonis Mons. The linear and sinuous features mark the locations of lava tubes and graben that occur on both sides of the volcano … Continue reading
Posted in Reports
Tagged Arizona State University, ASU, lava channels, lava flows, lava tubes, Mars Odyssey, NASA, Pavonis Mons, Tharsis, THEMIS, THEMIS Image of the Day, Thermal Emission Imaging System, volcanics
Comments Off
THEMIS: Collapse features on flank of Ascraeus Mons
THEMIS Image of the Day, September 5, 2017. This image shows part of the northeastern flank of Ascraeus Mons, along the trend that joins the three large Tharsis volcanoes. The image has a myriad of collapse features from circular to … Continue reading
Posted in Reports
Tagged Arizona State University, Ascraeus Mons, ASU, collapse features, collapse pits, lava channels, lava flows, Mars Odyssey, NASA, Tharsis, THEMIS, THEMIS Image of the Day, Thermal Emission Imaging System, volcanics, volcanism, volcanos
Comments Off
THEMIS: Pit craters on Ascraeus Mons
THEMIS Image of the Day, September 4, 2017. This image shows a collapse feature on the southeastern flank of the volcano. The circular/scalloped margin of the collapse is typical for ceiling collapse into a lava tube. However, the potential lava … Continue reading
Posted in Reports
Tagged Arizona State University, Ascraeus Mons, ASU, graben, lava channels, lava flows, Mars Odyssey, NASA, pit craters, tectonics, Tharsis, THEMIS, THEMIS Image of the Day, Thermal Emission Imaging System, volcanics, volcanism, volcanos
Comments Off
THEMIS: Collapsed lava channel on Ascraeus Mons
THEMIS Image of the Day, September 1, 2017. This image shows part of the southern flank of Ascraeus Mons. The feature at the bottom of the image is a collapse feature. These features can be caused by several processes. The … Continue reading
Posted in Reports
Tagged Arizona State University, Ascraeus Mons, ASU, lava channels, lava flows, Mars Odyssey, NASA, Tharsis, THEMIS, THEMIS Image of the Day, Thermal Emission Imaging System, volcanics, volcanism, volcanos
Comments Off
THEMIS: Lava levees on Ascraeus Mons’ upper slopes
THEMIS Image of the Day, August 31, 2017. This image of the flank of Ascraeus Mons shows several individual flows where the sides are higher than the center. These are called leveed flows, as the outer margin acts as a … Continue reading
Posted in Reports
Tagged Arizona State University, Ascraeus Mons, ASU, lava channels, lava flows, lava levees, Mars Odyssey, NASA, Tharsis, THEMIS, THEMIS Image of the Day, Thermal Emission Imaging System, volcanics, volcanism, volcanos
Comments Off
THEMIS: Flows and faults on Ascraeus Mons
THEMIS Image of the Day, August 29, 2017. Looking again at the southeastern flank of the volcano the narrow nature of the flows are visible. Given the steep sides of the volcano, flows from the summit run as narrow “rivers” … Continue reading
Posted in Reports
Tagged Arizona State University, Ascraeus Mons, ASU, faulting, faults, lava channels, lava flows, Mars Odyssey, NASA, Tharsis, THEMIS, THEMIS Image of the Day, Thermal Emission Imaging System, volcanics, volcanism, volcanos
Comments Off